390. Анаграммы

Анаграммой слова называется любая перестановка всех букв слова. Например, из слова SOLO можно получить 12 анаграмм: SOLO, LOSO, OSLO, OLSO, OSOL, OLOS, SLOO, LSOO, OOLS, OOSL, LOOS, SOOL.

Напишите программу, которая выводит количество различных анаграмм, которые могут получиться из этого слова.

Вход. В единственной строке задано слово, количество букв в котором не превышает 14.

Выход. Количество различных анаграмм.

Пример входа	Пример выхода
SOLO	12

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Пусть мультимножество содержит n₁ элементов a₁, n₂ элемента a₂, … , n_k элементов a_k. Тогда число его перестановок равно полиномиальному коэффициенту

P(n₁, n₂, …, n_k) = = ,

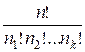где n = n₁ + n₂ + … + n_k – общее число элементов в мультимножестве.

Вычислим количество перестановок мультимножества, используя сочетания: n₁ элементов a₁ можно расположить на n местах способами. На следующих n – n₁ оставшихся местах можно расположить n₂ элементов a₂ способами. Рассуждая подобным образом, получаем, что n_k элементов a_k можно расположить способами. Согласно правилу произведения имеем:

P(n₁, n₂, …, n_k) = * * … * =

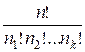
Реализация алгоритма

Читаем входную строку, сортируем буквы в лексикографическом порядке. Изначально положим res = len!, где len равно длине строки.

gets(s); len = strlen(s);

sort(s,s+len);

c = 1;

res = fact(len);

Для каждого набора подряд идущих букв вычисляем его длину c. Делим значение len на c!.

for(i = 0; i < len - 1; i++)

if (s[i] == s[i+1]) c++;

else

{

res /= fact(c);

c = 1;

}

res /= fact(c);

Выводим результат res.

printf("%lld\n",res);